教学内容：

《数学》五年级上册第30～32页例1、“试一试”“练一练”，练习五第1～16题。

教学目标：

1．使学生在现实情境中认识小数的意义，学会读、写小数，体会小数与十进分数之间的联系。

2．使学生在认识小数的过程中，体会数学知识之间的联系和数的扩展，培养观察比较、综合归纳和抽象概括等思维能力，进一步发展数感。

3.使学生主动思考，体会数的不同表达方式，在理解、认识小数意义的过程中提高学好数学的信心。

教学重点：认识小数的意义。

教学难点：如何通过观察、比较，抽象概括出小数的意义。

教学过程：

一、谈话导入，感受小数产生的必要性

师：课前老师问了几位同学的身高，有的说1.65米，还有的说大约1.6米。

导语：在进行测量或计算时，像这样不能正好得到整数的结果，我们常常用小数来表示。

在三年级时我们已经初步认识了小数，今天我们进一步来认识小数。

二、理解生活中的小数，初步感知小数的意义

1.小数的读写。

（出示：一块橡皮0.3元     一张邮票 0.05元     一本本子0.48元）

师：这些都是什么数？谁能来读一读。

小结：注意读小数的时候，小数点后面的数要按顺序一个数字一个数字地读。

师：谁还记得小数各部分的名称？（中间的小圆点叫小数点，小数点左边是整数部分，右边是小数部分）

师：小数部分是一位的小数叫作一位小数。小数部分是两位的小数叫作两位小数。

观察：上面这些小数哪些是一位小数，哪些是两位小数？

2.在具体情境中初步感知小数的意义

（1）理解人民币单位中的小数。

师：如果老师要买这些东西，该怎样付钱呢？

一块橡皮0.3元，该怎样付钱？你会写成用元作单位的分数吗？为什么？

师：那么0.05元、0.48元又该怎样付钱呢？你会写成用元作单位的分数吗？为什么？

你能把下面各数写成用元作单位的分数和小数吗？

7角＝（  ）元＝（  ）元      35分＝（  ）元＝（  ）元

9角＝（  ）元＝（  ）元      68分＝（  ）元＝（  ）元

仔细观察你发现了什么？

（2）理解长度单位中的小数。

师：（出示米尺）把1米平均分成10份。每份有多长？用米作单位是几分之几米？为什么？写成小数又是多少米？

5分米等于几分之几米，写成小数又是多少？ 0.7米表示几分之几米？有多长？

师：如果把1米平均分成100份，每份有多长？

同样用米作单位1厘米就是几分之几米？为什么？还可以写成怎样的小数呢？（米可以写成0.01米；0.01米就表示米）

师： 35厘米等于几分之几米？写成小数又是多少米？谁能完整地说一说。那0.78米表示几分之几米？有多长呢？

你能把下面各数写成用米作单位的分数和小数吗？

7分米＝（ ）米＝（ ）米    7厘米＝（ ）米＝（  ）米

3分米＝（ ）米＝（ ）米　　62厘米＝（ ）米＝（　）米

通过观察你发现了什么？

三、数形结合，抽象小数的意义

1.抽象概括出一、两位小数的意义。

（1）出示：   0.7元   0.02元     0.9元      0.68元   

0.6米   0.07米     0.8米      0.92米

师：我们已经认识了这些小数的实际意义，找一找上面哪个小数能与左边的图对应？哪个小数能与右边的图对应？为什么？

（2）出示：    0.7      0.02      0.9      0.68

               0.6      0.07      0.8      0.92

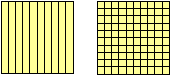
师：现在我们把单位名称去掉，如果把每个正方形都看作整数1，把上面这些小数分分类，哪些小数你会选择左边的图来继续表示？哪些小数选择右边的图来继续表示？为什么？

（3）思考：分母是多少的分数可以写成一位小数，一位小数表示几分之几？分母是多少的分数可以写成两位小数，两位小数又表示几分之几？

2.迁移类推出三位、四位小数的意义。

（1）（出示）

师：如果仍把正方形看成整数1，想象一下该如何表示三位小数？你能举个三位小数的例子，并说说怎么表示吗？

（2）思考：分母是多少的分数可以写成三位小数，三位小数表示几分之几？

（3）继续想象：分母是多少的分数可以写成四位小数，四位小数表示几分之几？还能否继续往下说？说得完吗？

3.归纳概括小数的意义。

师：现在谁能完整地说一说：分母是多少的分数可以用小数来表示？一位小数表示什么？两位小数表示什么?三位小数表示什么？

4．有序数数，沟通整、小数之间的联系。

（1）师：把正方形看成整数1，平均分成10份可以得到哪些一位小数？我们一起来数一数。最小的一位小数是多少？ 0.9里面有几个0.1，在加一个0.1是多少？

（2）把正方形平均分成100分又可以能到哪些两位小数？我们同样也一起来数一数。最小的两位小数是多少？0.1里面有几个0.01,再加１个0.01是多少？

（3）在数的过程中你有没有发现小数与整数有什么相同点？

（4）小结：从右往左：10个0.01是0.1，10个0.1是1，10个1是10，10个10是100，还能这样累积吗？小数和整数一样都是满十进一。

从左往右，也就是把1平均分成10份，得到10个0.1，把0.1平均分成10份得到10个0.01，把0.01平均分成10份，可以得到10个0.001，还能细分吗？反过来同样都是退一当十。

四、拓展应用，加深对小数意义的理解

1.下面每个正方形都表示整数“1”，图中涂色部分用小数表示是多少？为什么？

      （    ）     （    ）        （       ）

2. 你能在数轴上找到上面这些小数所对应的点吗？

师：0.3在几和几之间？它对应的点在哪里？

0.14又在几和几之间？ 怎样找到它所对应的点？（根据学生的回答，师把0.1和0.2之间的一段再平均分成10份）现在能找到它对应的点了吗？

3. 2.3在几和几之间？它对应的点又在哪里？想象：200.3在几和几之间？ 2000.3呢？还能大吗？

4. 现在你觉得小数小吗？在什么情况下我们会用小数来表示？

五、本课总结

通过今天这节课的学习，你对小数又有了怎样的新认识。