江苏省海安县城南实验小学         唐小琴

【摘要】数学作为一门理性学科，就会存在着许多规定，而低年级学生的数学学习具有直观性、语言表达能力还未成熟等特征。我们该如何让孩子从单一枯燥的数学规定走向深度思考呢？又怎样让这些抽象的规定在孩子们的心中得到完美内化？本文从“释疑”“ 举例”“ 还原”这些角度阐释了对数学规定教学的一些认识。教师应结合低年级孩子的生理和心理特点，帮助学生了解规定的背景，感受规定的合理性，体会规定的道理，真正地将知识内化、吸收并运用自如。

【关键词】规定 内化  

小学一二年级是数学学习的基础阶段，这个阶段对孩子整个一生的学习和长远发展都有着举足轻重的作用。但即使是低年级的孩子，只要进行数学学习，就会经常遇到一些数学规定，例如：满十进一、退一当十、从个位算起……这些规定似乎是枯燥的、硬邦邦的，难以理解的。事实上，数学里的这些规定都是有根可挖，有源可思的。此时，教师如果陪着孩子一起去领略规定的风景，了解规定的背景，感受规定的合理性，体会规定的道理。一旦将这些规定说清了，道明了，那给孩子留下的将是无限的数学魅力和震撼力。孩子们在学习数学时也一定更具有主动性、探究性、创造性和趣味性，而不是早早地对数学产生畏惧心理。本人试着从以下几个方面谈谈自己的思考。

    一、释疑——感受为什么这么规定

虽然课改之后，数学的一些规定，不再用文本的形式呈现出来，但教师仍会不时地补充这些规定并让孩子熟记，因此孩子们还是无形地感受到数学的一些规则是记忆的。数学家的确做了许多规定，问题是数学家为什么要这么规定？如果我们愿意花时间陪着孩子一起了解，这样学生就能体会数学规定的合理性，从而也可以让学生在充分了解的基础上理解规定，起到事半功倍的作用。

学习一年级下册两位数加两位数（进位加）时，学生在理解了算理的基础上，自主探究笔算的写法。由于孩子们已经有了两位数加两位数（不进位加）笔算的经验，大家对笔算加法的书写格式了如指掌，于是都信心十足地尝试起来（如图1、图2、图3）。

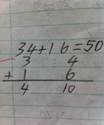
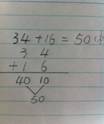
                  图1                图2                        图3  

仔细观察这3种写法，孩子们都在自己的理解上创造了进位加。虽然写法不同，但从横式的结果可以看出孩子们都理解了50的由来。但由于每个人的写法各不相同，规定两位数加两位数笔算写法自然成了大家内在的迫切需要。在这种情境下，教师立即引导学生，你觉得自己在笔算这道题时，最大的困惑是什么？孩子们不约而同地提到个位上4+6=10,这个10不知道该怎么写？此时的困惑是孩子们思考的加速器，教师立即组织孩子们兴高采烈地讨论10的各种写法。也许不经过预习的学生不可能想到书上的那种写法，但学生在亲自尝试后找到了问题的困惑。也只有亲自感受到了困难，再经历讨论和思考这个过程之后，回过头来反思书本上规定的写法。此时无需过多的赘述，孩子们把自己的写法和书上的进行比较的同时，轻松自然地理解了为什么10这么写？（因为10是两位数，不好直接写在个位的下面，所以在个位写0，十位写1）。只有亲身经历思考10怎么写，才能真正地体会10为什么这么写。此时这种智慧、简洁的笔算写法就如一缕阳光，让孩子们顿时豁然开朗，给孩子心灵留下了无穷的神奇和震撼力！因此即使是一年级的孩子，也可以真正地把一节技能的训练课提升为思维发展课。

当然，像这样的例子还有很多，有的教师每次做到笔算时，总是反复地强调：要数位对齐，从个位算起。天天强调，但结果却令人失望。因为学生无法体会从个位算起与从十位算起的孰优孰劣，为什么不让学生试着从十位算起（尤其是进位加），先写好十位的得数，再算个位时，由于满十进一，真切地感受十位还要擦掉重写的麻烦，体会从个位算起的合理性。

所以对于一年级的学生，即使一些枯燥的数学规定也可以让学生自己去理解、探索、思考，实现自我建构的良性循环。一旦给学生提供了自我活动的时空和创造的空间，孩子学习的想象力就会淋漓尽致地释放出来，学习局面也就会异彩纷呈。教师只有引导学生真正的释疑，理清为什么，他们才真正将知识内化、吸收，转换为自己的知识，运用自如。正如俞正强老师所说：道理的慢其实不是慢，是数学的核心；而知识的快不是快，是省略数学内涵。

二、举例——帮助学生理解规定

有些规定，对于小学生，尤其是低年级的孩子很难说得清，道的明。如果我们教师能根据学生的心理发展规律让一个个规定变得形象，变得多彩，变得丰满。那么孩子们理解这些僵硬的规定的过程便也会变得有趣、多维、立体。他们的学习过程也就变得积极、主动，而这不正是我们数学学习所需要的吗？

1.      运用直观形象的比喻理解规定

一年级下册学习口算退位减，如34-8，教师引导学生借助于学具来理解，当时课前预想的是个位上4里面不好拿走8，先拆一捆10根，再和4根合起来从14根里拿走8根。但出乎我的意料，课堂上孩子们习惯的是先拿走4根小棒，还差4根，再从任意一捆小棒里抽走4根，还剩26根；同样46-8，个位上6不好减8，孩子们习惯先拿走6根，还差2根，只好从其中的一捆小棒中抽走2根，还剩38根。当时课堂生成的是孩子们习惯差几根再借几根的思维模式（这与平时用完了再借的生活经验有关）。顿时直觉告诉我借助于小棒，孩子不能很到位地感受退一当十的数学思想。于是我立即进行调整，选择最合适的学具——计数器，感受退一当十的数学思想。但这对于一年级小朋友理解退一当十仍然比较抽象，我立即打了一个形象的比喻：十位的老爷爷年级大了，个位一会儿借4，一会儿借2，老爷爷根本记不住，老爷爷想了个办法，要么不借要借就借1捆，1捆就是10根，可老爷爷还是怕忘记了，每次借给别人一个十都在自己的头上点个小圆点做记号，乐得小朋友哈哈大笑。在笑声中初步渗透借一当十的想法。当然，退一当十的数学思想，并不是一节课就能让学生深刻感受的，孩子们需要借助于形象慢慢积累。孩子的数学经验需要经历一个从模模糊糊到逐步清晰再到豁然开朗的过程，在这个过程中，学生首先要认识，再通过练习和自己的思考不断糅合后才能最终接受并理解这个知识点。而这个生动的比喻为孩子体会退一当十提供了有力的支撑点。

2.      依靠生活经验理解规定

对于低年级学生来说，已有的生活经验是他们认识和理解数学重要的资源库，它对儿童的数学学习起着巨大的推动作用。因此在帮助一年级的孩子理解被减数、减数、差之间的关系时，我苦苦思索着怎样让孩子理解被减数一样，减数越小，差越大这种复杂的关系呢？此时何不依靠学生的生活经验，选取最贴近生活的例子：如妈妈给了你58元零用钱（被减数），你用的多（减数），那么剩下的钱就越少（差），你用的少，那么剩下的钱就越多。通过浅显的生活经验，不仅让孩子理解了三者之间的关系，还无形中渗透了理财的教育，真可谓一举两得！

3.      借助具体情境理解规定

以前在学习简单加减混合的算式时，书本上就会出现一句总结性规定：算式里有加有减，直接从左往右算。但学生能理解为什么要从左往右算以及从左往右的必要性吗？我们不得而知。在新课改之后，教材中不再出现这样总结性的规定，之所以进行这么大的变动，其目的在于避免教学的僵化和学生的死记硬背。新课改要求教师鼓励和引导学生在自己经历探索、理解的基础上建构规定。因此我们可以借助书上给出的上下车、买衣服等一些具体情境，让学生结合情境说清每一步算式所表示的具体含义，从而帮助学生在情境中理解了在同一级运算中要从左往右算这个规定背后的涵义。

对于低年级的小朋友，通过举例、具体情境将数学那种严密的逻辑关系辅以生动活泼的比喻、生活原型学习，使一个个枯燥干涩的数学规定演绎的生动起来，孩子们思维也自然地越来越活跃起来。孩子的思维活跃了，那么他们思维的广度、深度和密度就会得到不同程度的发展，学生也会更乐意投入到现实的、探索性的数学活动中去。

三、还原——按前人发现的过程再现规定

著名数学教育家弗赖登塔尔曾经这样描述数学的表达形式：“没有一种数学的思想,以它被发现时的那个样子公开发表出来,一个问题被解决后,相应地发展为一种形式化技巧,结果把求解过程丢在一边,使得火热的发明变成冰冷的美丽。”的确，我们学习的都是前人经过总结的间接经验，这些间接经验一般以结果的形式呈现，但这些对于低年级孩子来说有些单一、枯燥。我们应当避免孩子直接接受这些知识，而是尽可能地让孩子也尝试着还原经历发现的过程，这样的学习才更有意义。

1.      在认知冲突中还原规定

曾记得特级教师黄世忠老师在教学“数的产生和十进制”一课时，从古时候用石头计数开始，引导学生思考“如果我放出去千千万万只羊，用石头计数将会有什么后果?”孩子大胆发挥想象，猜测或许没有这么多石头，或许石头太多了就会堆成一座小山等许多的情况。在此基础上引出绳子打结计数法，当介绍完这种方法时，孩子们立即批判性地提出“结要越打越多，绳子又没那么长，又该怎么办呢？”接着引出画一横做记号直到后来的数的出现以及十进制的产生。刚开始还是教师引导学生思考，可后来学生渐渐地能自觉反应出以前一些计数法的利弊，并且在数产生的基础上理解了十进制的规定。整整一节课，孩子们的思维在不断的认知冲突中螺旋上升。其实孩子们这样的认知冲突过程正是当时各种计数法和十进制所经历的一步步的产生和形成的过程。但教师给足时间让学生真正参与和还原了“数和十进制的产生过程”的思考，在思考的过程中他们的思维才会情绪，记忆才会更深刻，否则教师讲的遍数再多也无济于事。

2.      在动手实践中还原规定

有些数学规定在我们成人眼里是理所当然的，但即使是这些最简单的数学规定，教师也应该给足时间让学生动手实践，探讨发现。在二年级认识直尺这节课上，完全可以模拟直尺的发现、制造过程，让学生动手制造直尺。先出示一个长方形框子（直尺的模型），让学生在模型上标出数据，体会为什么起点不从1开始而是从0开始标起，感受0作为起点的意义和读数的方便性。确定了0作为起点后，请学生接着画起点，在画起点时，大部分孩子选择在尺板的最左端画0。此时教师故意碰掉孩子们画出的尺板左边一点点，或出示一些用过的直尺，直观感受尺板的左右两端最容易磨坏，再讨论决定把起点往后依一点点。这个过程既解决了为什么起点不在尺板的最顶端，也解决了学生测量物体时不从起点开始而是从头量起的错误习惯。最后，用学生画出的直尺测量物体时，发现仅仅用整厘米无法准确测量物体的长度，深切感受了补充毫米甚至更小单位的必要性。孩子们在一步步的矛盾、思考和调整中还原了做尺的过程。无形中感受从量变到质变的过程。

因此数学的规定中潜蕴着丰富的自由思维，数学教学应当尽量地教“活”。尤其对于低年级学生，如果把数学教成形式严格、思想固化的另类东西，这样意味着过早地把孩子拒之数学学习门外。我们应该在尊重数学知识的基础上，可以让数学规定更生动些、有趣些、丰满些，这样不仅让孩子知其然更能知其所以然，也只有这样能让低年级孩子喜欢数学、热爱数学。总之数学不是记出来的，酷爱、理解才是数学学习的持续内动力。